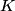 x-rays are released when an electron transitions to an x-rays are released when an electron transitions to an 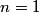 orbital from a higher orbital. The energy released is orbital from a higher orbital. The energy released is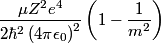 where 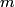 is the shell of the higher orbital. We are given that is the shell of the higher orbital. We are given that 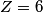 for carbon and for carbon and 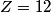 for magnesium, so the desired ratio is for magnesium, so the desired ratio is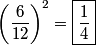 Therefore, answer (A) is correct. |